réponse simple
Réponse simple :
Concernant les jeux d’argent, qu’il s’agisse de machines à sous, de billets de loterie ou de papiers à gratter, la moyenne des gains est toujours inférieure à celle des pertes1. Cela signifie que, sur un nombre significatif de parties, le joueur perd forcément de l’argent, peu importe comment ses pertes et ses gains se sont répartis au cours du jeu2.

On dit que l'espérance est négative lorsque le bilan est toujours inférieur à 0 à long terme
Plus le nombre de parties augmente, plus ce fait est vérifié. Autrement dit : plus vous jouez, plus vous perdez d’argent. C’est la somme formée par les pertes de tous les joueurs qui contribue à l’enrichissement du casino.
Cette inégalité est généralement représentée par le « taux de redistribution », qui correspond à l’argent que la machine vous rend par rapport à l’argent qu’elle reçoit3. Un taux de redistribution de 85% signifie donc que vous perdez en moyenne 15% de votre mise.

Le taux de redistribution correspond au pourcentage de perte (sources multiples et modifiées)
Les casinos utilisent parfois cette information à but publicitaire, laissant le joueur imaginer à tort qu’il s’agit de ses chances de gains au lieu de son taux de perte.
Malgré ce fait établi, les joueurs continuent de se rendre au casino ou d’acheter des billets de loterie, car ils espèrent que leurs pertes moyennes seront compensées au final (après un grand nombre de parties) par un jackpot. Cette croyance est induite par une mauvaise notion des probabilités qui se trouve être faussée en deux points :
1) Les chances de gagner le jackpot sont bien plus faibles qu’on ne peut le concevoir
A titre indicatif, les chances de gagner le gros lot à l’Euromillions sont d’une sur 116 millions4, soit inférieure à la probabilité de trouver du premier coup un code à huit chiffres.

Il faudrait plus de dix ans pour essayer toutes les combinaisons possibles à 8 chiffres (source)
Nous imaginons qu’il suffit de jouer une centaine de parties pour avoir des chances significatives de gagner, or ce chiffre est plus d’un million de fois inférieur aux valeurs réelles.
2) D’une partie à l’autre, les probabilités ne s’additionnent pas
Lorsque vous tirez un dé, vos chances d’obtenir un six sont exactement d’un sixième. Si vous jouez une seconde fois, vos chances seront encore et toujours de la même valeur, elles n’augmentent pas d’après l’historique de vos parties. Il est donc tout aussi probable d’obtenir uniquement des six durant tout le jeu que n’importe quelle autre combinaison.
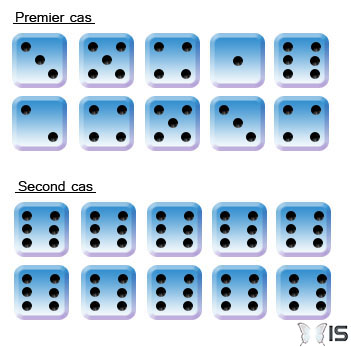
Difficile à croire, mais ces deux cas ont exactement la même chance de se produire
Cette vision est difficile à admettre, car nous concevons faussement le hasard comme une répartition homogène (voir cet article). Il nous semble donc logique qu’après avoir perdu une partie, nous ayons d’avantage de chance de gagner la suivante (d’où le fameux « encore une petite pièce… »).
D’un autre côté, s’il est vrai que nos chances d’obtenir le jackpot augmentent avec le nombre de parties, cet accroissement est moins rapide qu’il n’y parait. En effet, sachant qu’il faudrait jouer 34 millions de billets pour avoir 25% de chances de gagner à l’Euromillions, on s’attendrait à ce que doubler ce nombre multiplie également nos chances par deux. En réalité, les calculs nous montrent qu’il faudrait non pas 68 millions, mais 81 millions de billets pour avoir 50% de chances de gain. Nous avons donc une vision faussée de l'évolution des probabilités selon le nombre de parties.

Graphique réalisé sur la base d'un jackpot de probabilité 1/1'000'000
(avec une probabilité inférieure, le nombre de parties nécessaires augmente pour un même pourcentage)
Vu que chaque partie coute deux francs et que le jackpot est aux alentours de 40 millions4, il faudrait dépenser en moyenne 162 millions et jouer durant des années pour avoir une chance sur deux d’obtenir le jackpot, ce qui nous ferait perdre au minimum 122 millions sans compter l’imposition sur les gains.
Sauf rare exception, la recherche d'un jackpot ne compensera donc jamais les pertes d’un joueur habitué, qui sont par ailleurs inévitables au vu de l’iniquité des jeux d’argent.
réponse avancée
Réponse avancée :
L’équité d’un jeu d’argent peut être mesurée à l’aide d’une notion mathématique, appelée espérance1.
Les jeux d’argent possèdent plusieurs issues possibles qui correspondent soit à une perte soit à un gain monétaire. Par exemple, dans le cas d’une machine à sous, certaines combinaisons rapportent gros et d’autres pas le moindre centime.
Considérons un jeu d’argent à n issues possibles, dont les valeurs s’appelleront x1, x2, … xn. Si par exemple on a x2 = 4 et x5 = -10, cela signifie que le résultat 2 vous fait gagner 4 francs et le résultat 5 vous fait au contraire perdre 10 francs.
Chaque résultat possède une certaine probabilité de se réaliser. On notera p1 la probabilité que le résultat 1 se produise et ainsi de suite. A partir de ces données, l’espérance mathématique du jeu en question peut être définie comme suit1 :

Ce qui correspond à la valeur moyenne que va recevoir le joueur à la fin de chaque partie, c’est-à-dire son bénéfice moyen à long terme.
Si ce bénéfice est supérieur à 0, le jeu est favorable au joueur. Au contraire, s’il est négatif, le jeu est favorable à son adversaire (qui est souvent représenté par le casino). Dans le cas où ce bénéfice est nul, on dit alors que le jeu est équitable, car la moyenne pondérée des gains équivaut celle des pertes d’un côté comme de l’autre.

On dit que l'espérance est négative lorsque le bilan est toujours inférieur à 0 à long terme
En guise d’illustration, imaginons un jeu de dés avec la règle suivante.
- Résultat 1 : Tirer 1 : vous gagnez 15.-
- Résultat 2 : Tirer 2 ou 3 : vous gagnez 5.-
- Résultat 3 :Tirer 4, 5 ou 6 : vous perdez 10.-
Selon la formule ci-dessus, l’espérance de ce jeu vaut :
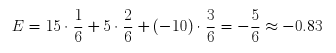
Cela signifie que vous allez perdre en moyenne 83 centimes par partie.
Comme l’espérance représente une moyenne, elle ne prend sens qu’après un nombre significatif de parties. Vous pouvez donc très bien gagner deux fois 15 francs aux deux premières parties, ce qui ne correspond pas à l’espérance, par contre, plus vous jouez, plus les gains et les pertes se compensent, faisant tendre la moyenne vers l’espérance, ici – 83 centimes.
Dans cet exemple, le jeu n’est donc pas équitable car vous avez tendance à perdre de l’argent. On peut d’ailleurs dire que plus vous jouerez plus vous perdrez d’argent.
Cette affirmation est également valable dans le cas des machines à sous, car, l’objectif des casinos étant de faire du profit, il est logique qu’ils proposent des jeux dont l’espérance sera négative pour le joueur2. Étant donné que le nombre de joueurs est grand, la moyenne des pertes de chaque joueur va correspondre assez fidèlement à l’espérance qu’ils ont fixée, leur assurant ainsi un bénéfice de taille.
Cette espérance n’a pas besoin d’être élevée. En effet, si on suppose une espérance de – 1 franc pour le joueur (donc de +1 pour le casino) et qu'un million de personnes jouent, le casino sera assuré de gagner une somme proche d’un million de francs. Dans la pratique, le casino devra sûrement payer de forte sommes pour les vainqueurs du jackpot, mais ces rares dépenses seront largement compensées par la multitude des autres joueurs perdants.
Les casinos préfèrent souvent parler de taux de redistribution plutôt que d’espérance. Cette notion similaire correspond à l’argent que la machine vous rend par rapport à ce que vous avez misez3. Un taux de redistribution de 85% signifie ainsi que 15 % de votre argent misé sera perdu au profit du casino.

Le taux de redistribution correspond au pourcentage de perte (sources multiples et modifiées)
Ces informations sont parfois utilisées à but publicitaire, laissant le joueur imaginer à tort qu’il s’agit de ses chances de gains au lieu de son taux de perte.
Même si les chiffres sont clairement en défaveur des joueurs, de nombreuses personnes continuent de se rendre au casino ou d’acheter des billets de loterie, car ils ont toujours l’espoir que leurs pertes seront compensées par un jackpot. Cette croyance est induite par une mauvaise notion des probabilités qui se trouve être faussée en deux points :
1) Les chances de gagner le jackpot sont bien plus faibles qu’on ne peut le concevoir
Par exemple, les chances de remporter le gain maximum à l’Euromillion sont d’une sur 116 millions4, soit inférieure à la probabilité de trouver du premier coup un code à huit chiffres.

Il faudrait plus de dix ans pour essayer toutes les combinaisons possibles à 8 chiffres (source)
Nous imaginons qu’il suffit de jouer une centaine de parties pour avoir des chances significatives de gagner, or ce chiffre est plus d’un million de fois inférieur aux valeurs réelles.
2) D’une partie à l’autre, les probabilités ne s’additionnent pas
Lorsque vous tirez un dé, chaque lancé est indépendant des précédents. Ainsi la probabilité d’obtenir un six à votre premier lancé est exactement la même que celle d’obtenir un six au deuxième lancé. Il est donc tout aussi probable d’obtenir uniquement des six durant tout le jeu que n’importe quelle autre combinaison.

Difficile à croire, mais ces deux cas ont exactement la même chance de se produire
Il en va de même pour les machines à sous. Le fait que vous ayez perdu ou gagné à une partie n’influencera en rien la partie suivante. Cette vision est difficile à admettre, car nous concevons faussement le hasard comme une répartition homogène (voir cet article). Nous nous attendons donc à tort à ce qu’un gain succède à une perte.
D’un autre côté, s’il est vrai que nos chances d’obtenir le jackpot augmentent avec le nombre de parties, cet accroissement est moins rapide qu’il n’y parait. Certaines personnes ont l’impression que si elles jouent deux fois, leur chance de jackpot double, ou qu’elle triple si elles jouent trois fois et ainsi de suite. Ce n’est malheureusement pas le cas.
Il est possible de calculer la probabilité P de gagner au moins un jackpot en jouant n parties consécutives, si la probabilité de gagner le jackpot sur une partie est de p. La formule est2 :

A l’euromillion, la probabilité de gagner le jackpot est de p=1/1165318004. On remarque donc que si l’on joue n = 33 millions de billets, on a alors seulement 25% de chance d’avoir au moins un jackpot sur tous ces billets. Contrairement à la vision intuitive, la probabilité P n’est pas linéaire, ce qui signifie qu’il ne suffit pas de jouer 66 millions de billet pour atteindre 50%, mais 81 millions de billets.

Quelle que soit la valeur de p (ici 1/1'000'000), l'écart entre les deux fonctions est toujours le même, avec un maximum de 37%
Ainsi un jackpot ne serait même pas suffisant pour compenser les pertes occasionnées. En effet, il faudrait dépenser 162 millions d’euro en billets pour avoir une chance sur deux de recevoir un jackpot dont le montant oscille autour de 40 millions d’euro4. Les pertes resteraient toujours d’au moins 122 millions d’euros, sans compter l’imposition sur les gains.
Sauf rare exception, la recherche d’un jackpot ne compensera donc jamais les pertes d’un joueur habitué, qui sont par ailleurs inévitables au vu de l’iniquité des jeux d’argent.








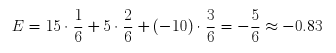



Commentaires
Bonjour Jipsira,
Je peux vous expliquer ici comment obtenir cette formule.
Le problème est le suivant. Vous jouez n fois à un jeu et à chaque fois vous avez une probabilité p de gagner. On se demande quelle est la probabilité de gagner au moins une fois.
« gagner au moins une fois » est l’inverse de « ne jamais gagner ». Donc P(« gagner au moins une fois ») = 1 – P(« ne jamais gagner »). Il suffit donc maintenant de savoir calculer la probabilité de ne jamais gagner, ou autrement dit de perdre à chaque fois. Or la probabilité de perdre une fois est de 1-p (l’inverse de gagner). Vu qu’on joue n fois et que les évènements sont indépendants, on va obtenir que la probabilité de ne jamais gagner vaut (1-p)(1-p)…(1-p) = (1-p)^n.
Donc au final on obtient bien 1-(1-p)^n.
JJ’espère que c’est assez clair.