réponse simple
Réponse simple :
Les nombres premiers sont des entiers qui possèdent exactement deux diviseurs distincts : 1 et eux-mêmes1. Ils appartiennent à l’ensemble des nombres entiers naturels, c’est-à-dire ceux avec lesquels nous avons l’habitude de compter.
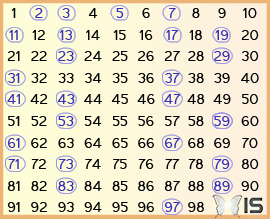
Les nombres premiers sont compris dans l'ensemble des nombres naturels
Le premier aspect à remarquer est qu’il n’existe pas de limite aux nombres entiers : quelque que soit le chiffre que l’on conçoit, on trouvera toujours un nombre supérieur à ce dernier (par exemple en lui ajoutant 1). On dit ainsi que l’ensemble des entiers naturels est infini7.

Il est potentiellement possible de compter jusqu'à l'infini
La question est maintenant de savoir combien on peut trouver de nombres premiers. Puisque l’ensemble des nombres naturels est infini, on peut intuitivement s’imaginer que celui des nombres premiers l’est également. Pour vérifier cette hypothèse, on utilise une démonstration dite « par l’absurde » : on suppose qu’il existe une limite aux nombres premiers et on observe les conséquences qui en découlent3.

Le raisonnement par l'absurde permet de prouver la véracité d'une hypothèse
Mathématiquement, ce postulat aboutit à une contradiction (voir niveau avancé pour plus de détails), ce qui nous prouve qu’il y a bien un ensemble infini de nombres premiers.
Ainsi, quel que soit le chiffre que vous imaginez, il existera toujours un nombre premier qui lui sera supérieur.
réponse avancée
Réponse avancée :
Les nombres premiers appartiennent aux entiers naturels7, un ensemble infini que l’on désigne par le signe  . Une notion fondamentale de ce domaine est la divisibilité8 :
. Une notion fondamentale de ce domaine est la divisibilité8 :

Dont l’une des propriétés que nous allons utiliser est :
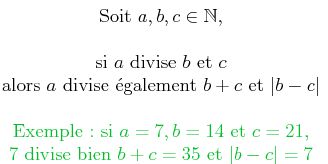
Par rapport aux autres nombres naturels, les nombres premiers ont la particularité de posséder exactement deux diviseurs distincts : un et eux-mêmes1. Remarquons que le chiffre 1 n’appartient pas à cette catégorie, vu qu’il ne possède en soi qu’un seul diviseur.
L’une des caractéristiques principales de ces nombres premiers est qu’ils peuvent servir à former n’importe quel nombre naturel. Il s’agit du théorème fondamental de l’arithmétique2 :

A partir de ce théorème, il est possible de prouver qu’il existe une infinité de nombres premiers. Ce résultat fut initialement établi par Euclide, vers 300 avant J.-C.6
La démonstration s’effectue par l’absurde ; supposons que l’ensemble des nombres premiers est fini3. Les éléments qui le constituent sont organisés par ordre croissant, pn étant l’hypothétique plus grand nombre premier :
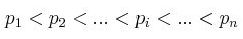
Pour la suite de notre raisonnement, nous créons le nombre N, un entier naturel résultant du produit de tous ces nombres premiers :

Ainsi que ce même nombre augmenté de 1 :

D’après notre hypothèse, N et N+1 ne peuvent pas être des nombres premiers vu qu’ils sont supérieurs à pn.
A partir du théorème fondamental de l’arithmétique, on sait que N+1 doit pouvoir être décomposé en un produit de nombres premiers (appartenant à p1, p2,…pi,… pn). Il existe donc au moins l’un de ces nombre qui le divise, appelons-le pi.
Comme pi est un nombre premier, il divise non seulement N+1, mais également N (formé du produit de tous les nombres premiers). Or, en se référant à une propriété de la divisibilité (voir plus haut), si pi divise N et N+1, alors il divise également (N+1)-N, ce qui est égal à 1. On a donc pi qui divise 1.
On se trouve face à une contradiction : d’une part, 1 n’est divisible que par lui-même et d’autre part pi est un nombre premier et ne peut ainsi pas valoir 1. Ce résultat nous conduit à rejeter l’hypothèse de départ, comme quoi l’ensemble des nombres premiers est fini. Il existe donc une infinité de ces nombres.
Bien que cette caractéristique soit connue depuis longtemps, certaines propriétés de ces nombres premiers suscitent encore aujourd’hui le questionnement des mathématiciens, surtout en ce qui concerne leur répartition. Malgré les conjectures établies (hypothèse de Riemann4), il n’existe pour l’instant aucune formule qui permette de calculer directement un nombre premier.
A l’heure actuelle, une des preuves formelles concernant la répartition des nombres premier est le postulat de Bertrand5 qui affirme que pour tout entier n supérieur à 1, il existe au moins un nombre premier entre n et 2n.





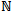 . Une notion fondamentale de ce domaine est la divisibilité
. Une notion fondamentale de ce domaine est la divisibilité

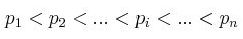


Commentaires
les accords, les gammes, l'harmonie, la modalité,
il est possible de les représenter toutes
mathématiquement comme des structures
rationnelles de nombres premiers.
Cette question des nombres premiers a fasciné des générations entières de mathématiciens depuis des millénaires et continue de les fasciner.
C'est particulièrement la difficulté de savoir si un grand nombre est premier ou non qui permet de crypter des messages et de s'assurer qu'ils ne puissent pas être décodés par des mauvais destinataires.
Pour plus de détails : fr.wikipedia.org/.../...